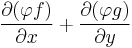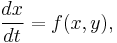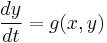Bendixson–Dulac theorem
In mathematics, the Bendixson–Dulac theorem on dynamical systems states that if there exists a function 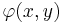 such that
such that
has the same sign (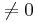 ) almost everywhere in a simply connected region, then the plane autonomous system
) almost everywhere in a simply connected region, then the plane autonomous system
has no periodic solutions. "Almost everywhere" means everywhere except possibly in a set of area 0, such as a point or line.
The theorem was first established by Swedish mathematician Ivar Bendixson in 1901 and further refined by French mathematician Henri Dulac in 1933 using Green's theorem.[1]